|
�可以看到最低阶项是Δx
的一次方项,我们可以将上式写为:
�
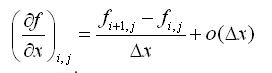
�舍弃 o(Δx),则可得到有限差分表达式:
�
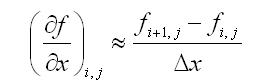
�其中舍弃的部分o(Δx)称为截断误差。可以看出该表达式的截断误差最低项是Δx的一次方,则称该有限差分格式具有一阶精度,由于该表达式仅仅用到了(ij)和(i+1,j)的信息,该格式称为一阶向前差分。
�再看(i-1,j)这个点的泰勒展开式为:
�
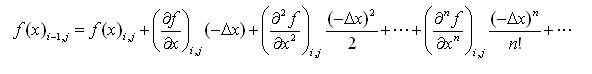
�与(i+1,j)点处的泰勒展开式相减可得:
�
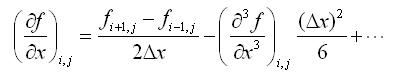
�即:
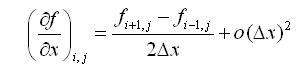
�可见该有限差分格式具有二阶精度,又由于用到了(i,j)左右两侧的信息,所以称为二阶中心差分格式。同理,根据以上思路,还能推导出精度更高的差分格式,这里就不再赘述。
|
