网格
�网格的作用
�前面提到过,计算流体力学(CFD)的任务就是求解NS方程,而求解该方程只能通过迭代方法得到其数值解,这就涉及到了微分的离散化等过程。前一节我们已经简要介绍了微分的离散化及其差分格式,可知微分离散化的关键因素之一就是
,这在几何上的表示就是很小的几何单元。
�网格就是由一系列离散点组成的区域,这些离散点组成的单元则成为网格单元。
�网格的作用就是将计算域划分成一个一个小的几何单元,然后根据差分格式就能求解相应的微分了。
�网格单元就相当于 Δx
,在这个网格单元中,物理量都认为是相等的。
�下面来看看这个例子,对于一个曲线,假设x在Δx范围内y值是相等的,且等于 f(x+Δx/2),我们来看看离散化中Δx
的大小对拟合结果的影响。
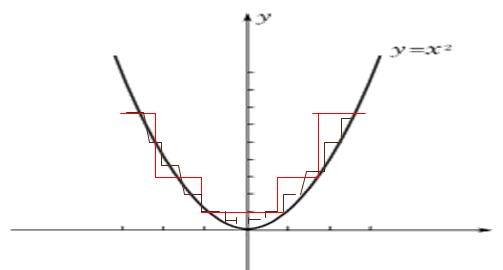
可以看出只要Δx
足够小,拟合出来的曲线就足够接近真实函数曲线
